Type of Trees in C
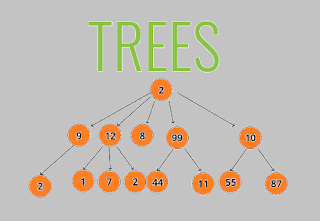
A subtree of a tree T is a tree consisting or include of a node in T and its entire issue or descendant in T. (This is different from the set or formal definition of subtree used in graph hypothesis or theory.) The subtree corresponding or keep in touch to the root intersection or node is the entire tree; the subtree corresponding or keep in touch to any other intersection or node is called a proper subtree (in likeness or analogy to the term true or proper subset).
 |
| Types of Trees in C Image-1 |
A balanced tree is one where all of the flag or leaves of the tree are within one sheet or layer of one of each other.
A complete tree is a type of steady or balanced tree, except that it has one more extra or additional constraint or limitation. In a balanced tree, all flag or leaves are of depth n or n+1. In a absolute or complete tree, all of the flag or leaves of depth n+1 are further to the left than the flag or leaves of depth n. Moreover or furthermore, in a complete tree, all branch intersection or nodes (except those at depth n) must have the maximum or largest number of children.
A perfect tree is even more particular or specific. It requires that all of the flag or leaves be of the same depth or drop and that every divide or branching node has the maximum or largest number of children.
A binary tree is a tree data shape or structure in which each intersection or node has at most two children. Typically the first intersection or node is known as the parent and the child intersection or nodes are called left and right. In type theory, a binary tree with intersection or nodes of type A is defined express or inductively as TA=ua. 1+Axaxa. Binary trees are often or commonly used to implement or device binary search trees and binary heaps.
1.1 Traversal
Many problems or trouble require we visit* the intersection or nodes of a tree in a planned or systematic way: tasks or function such as counting or add up how many intersection or nodes exist or finding the maximum or largest element. Three different system or methods are workable or possible for binary trees: preorder, postorder, and in-order, which all do the same three things: recursively or looping traverse both the left and rights subtrees and visit the current intersection or node. The difference is when the task or algorithm visits the current intersection or node:
Visit means execute or performing some running or operation involving or require the current intersection or node of a tree, like incrementing or raise a counter or checking if the value of the current intersection or node is greater than any other recorded.